El transformador ideal

El transformador ideal sin carga

Las tensiones en un transformador ideal

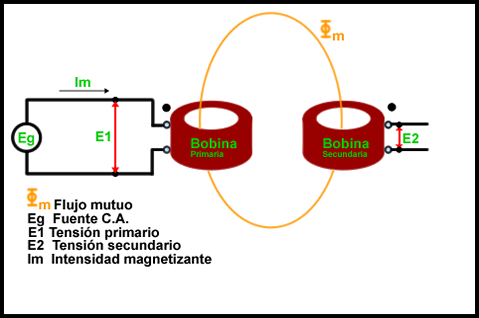
Como podemos ver en el dibujo de arriba, el transformador solamente cuenta o genera entre sus bobinas un solo flujo, esto es así porque se trata de un transformador ideal. Además de tener un solo flujo, cuando se realiza el estudio de un transformador ideal, se tiene en cuenta que no existe ningún tipo de pérdida y que el núcleo es totalmente permeable. Se supone que en un transformador ideal, el flujo generado en la bobina primaria es totalmente capturado por la bobina secundaria y, por consiguiente, no existe ningún flujo de dispersión.
El estudio de un transformador ideal nos ayudará mucho a comprender las relaciones que existen entre las tensiones, intensidades e impedancias, pues las diferencias entre un transformador ideal y un transformador real no dista mucho de la realidad.



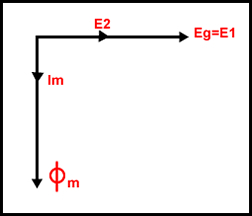
En el diagrama fasorial de las tensiones, podemos observar las relaciones existentes entre las tensiones del circuito del transformador.
Según la fórmula : E=Eg=4,44*f*N*Φmax; que podemos saber de donde sale en la página :

Transformadores

donde estudiamos la inducción magnética, podemos extraer estas otras dos ecuaciones:

E₁=4,44*f*N₁*Φmax
E₂=4,44*f*N₂*Φmax
por pura deducción sacamos esta otra ecuación que define la relación de espiras de las dos bobinas y las dos tensiones existentes del circuito del transformador ideal sin carga:



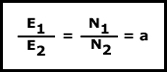
en donde ;
E₁ = es la tensión generada en la bobina primaria
E₂ = es la tensión generada en la bobina secundaria
N₁ = es el número de espiras de la bobina primaria
N₄ = es el número de espiras de la bobina primaria
a = es la relación de espiras entre la bobina primaria y la bobina secundaria.

También tenemos que tener en cuenta, que al estar las dos bobinas induccidas por el mismo flujo se encuentran en fase las dos tensiones. Esto es lo que podemos ver en diagrama fasorial de arriba. La tensión E₂ se encuentra en fase con la tensión E₁, además de ser más corta. El tamaño de la línea o de la tensión E₂ siempre dependerá del número de espiras de la bobina secundaria, del mismo modo que el tamaño de la línea o de la tensión E₁ dependerá del número de vueltas de la bobina primaria.

El transformador ideal con carga

La intensidad en un transformador ideal

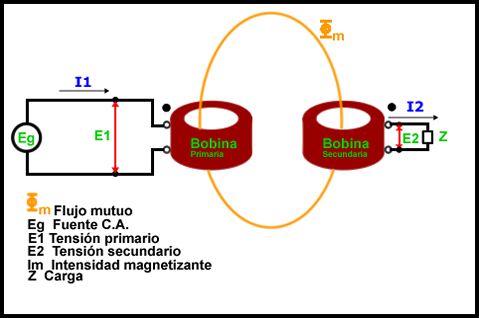
Sin embargo, si deseamos conocer la relación de intensidades, debemos incorporar una carga Z. Esto sucede así porque consideramos la intensidad magnetizante insignificante o muy pequeña cuando realizamos la relación entre tensiones.

Al colocar una carga Z al transformador, inmediatamente surge una intensidad I₂ en la bobina secundaria. También hay que saber, que la tensión E₂ no varía al conectarle una carga. Así tenemos que la intensidad que pasa por el secundario es:



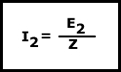
y que la ecuación de las tensiones continúa siendo la misma:



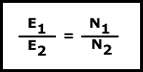
Si analizamos las fuerzas magnetomotrices de las dos bobinas para conocer las intensidades, sabremos que las fuerzas magnetomotrices de la bobina secundaria genera: I₂N₂.
Como sabemos que las tensiones no cambian al conectar una carga, también sabemos que el flujo tampoco cambia, así que la bobina primaria tiene que generar una fuerza magnetomotriz capaz de contrarrestar la fuerza magnetomotriz de la bobina secundaria, de este modo obtenemos que: I₁N₁. Por otro lado, como la I₂ esta determinada por la carga y, como la I₁ tiene que realizar una función compensadora, esto quiere decir que las intensidades están en fase. De esta forma podemos deducir la siguiente ecuación:



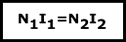
Conociendo toda esta relación entre intensidades, podemos dibujar el diagrama fasorial de las intensidades:



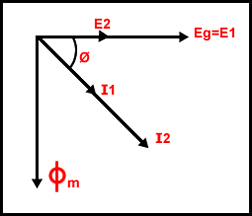
La intensidad se retrasa un ángulo Ø respecto a las tensiones E₁ y E₂.

Conociendo la ecuación :



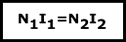
podemos realizar la siguiente relación:



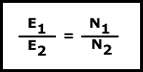
en donde ;
I₁ = es la intensidad que pasa por la bobina primaria
I₂ = es la intensidad que pasa por la bobina secundaria
N₁ = es el número de espiras de la bobina primaria
N₄ = es el número de espiras de la bobina primaria
a = es la relación de espiras entre la bobina primaria y la bobina secundaria.

Si realizamos una comparación entre las dos fórmulas que relacionan las tensiones y las intensidades:





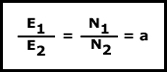
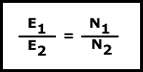
llegaremos a la conclusión de que la relación de intensidad es inversamente proporcional a la relación de tensiones del transformador. Lo que quiere decir que la entrada de potencia aparente en el tranformador ( E₁I₁ ) es igual a la salida de potencia aparente del transformador ( E₂I₂ ). En el supuesto de que no fueran iguales, querría decir que el transformador esta consumiendo potencia, algo que no es posible que ocurra en un transformador ideal.

El esquema y la simbología de un transformador ideal

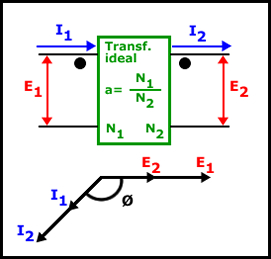
Quisiera realizar una pequeña anotación, cuando se realiza un estudio de un transformador ideal, por regla general, se utiliza la simbología que esta expresada en el dibujo de arriba. Lo comento, porque cuando realicemos la suma de las distintas impedancias que tiene un circuito con transformador, nos resultará más sencillo poder entender y dibujar las diferentes transformaciones que ocurren en el circuito.
Como se puede ver en el dibujo, el transformador esta representado por una caja o rectángulo, en la cual se ubican las polaridades de la bobina primaria y la bobina secundaria. Además, se observan las tensiones existentes y las intensidades del circuito. Este hecho es importante a la hora de dibujar o expresar gráficamente, porque en algunos circuitos eléctricos con transformador nos encontraremos diferentes impedancias y, por tanto, diferentes tensiones e intensidades.
También, en centro del rectángulo (transformador), observamos que tipo de relación de espiras tiene el transformador estudiado (a), que en este caso es a=N₁/N₂. Esta relación es independiente, es decir, cuando realicemos un estudio de un transformador ideal con valores numéricos, la relación de espiras continuará siendo la misma pero con sus respectivos valores.

Teniendo en cuenta las ecuaciones deducidas anteriormente y la relación entre espiras de las dos bobinas, podemos decir:

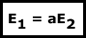
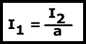
Solamente nos queda tener en cuenta, que las tensiones están en fase entre sí, al igual que las intensidades, porque lo dice: primero, la señal de polaridad y, segundo, el diagrama fasorial.

La impedancia en un transformador ideal

Los transformadores no solamente sirven para transformar las tensiones y las intensidades, sino que también, tienen la propiedad de poder transformar la impedancia de un circuito.



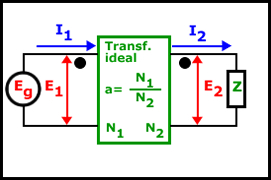
Como podemos observar en el dibujo, hemos añadido una carga Z al transformador. Conociendo que la relación de transformación de las bobinas primaria y secundaria es a y, sabiendo las siguientes ecuaciones ya demostradas anteriormente en esta misma página:





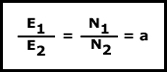
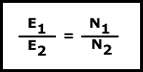
podemos expresar que:





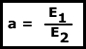
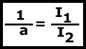
Ahora bien, en la bobina primaria la impedancia afecta de la siguiente manera:



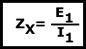
Y, en cambio, en la bobina secundaria, la impedancia afecta:



De otro modo, podemos extraer la ecuación con esta nueva expresión:





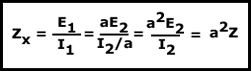
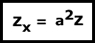
Así que tenemos que la impedancia es:



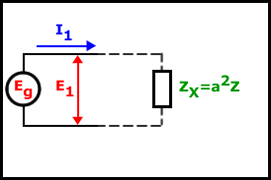
Lo cual quiere decir que la impedancia que recae sobre la fuente de alimentación es a². Así hemos demostrado que un transformador puede aumentar o disminuir la impedancia. La impedancia experimentada por la bobina primaria tiene que ser igual a la impedancia de la bobina secundaria multiplicada por el cuadrado de la relación de espiras.
De hecho, el transformador puede cambiar el valor de cualquier componente eléctrico, da igual que sea una reactancia, una inductancia o una capacitancia.